Matmol

Many physical and chemical processes are distributed parameter systems, i.e., systems in which state variables depend on several independent variables (such as time and space), and which are described by sets of nonlinear partial differential equations (PDEs).

The method of lines (MOL) is probably the most widely used approach to the solution of evolutionary PDEs, and the objective of this web site is to report on the development of a MATLAB based MOL toolbox.

Basically, the MOL proceeds in two separate steps:

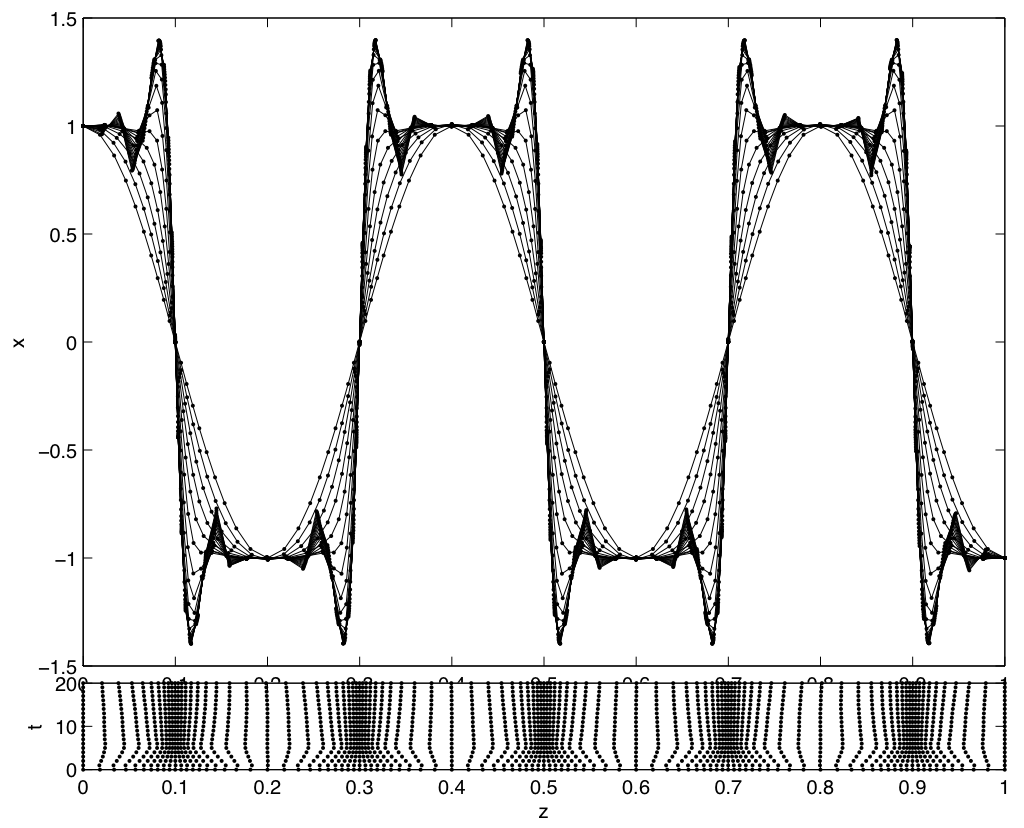
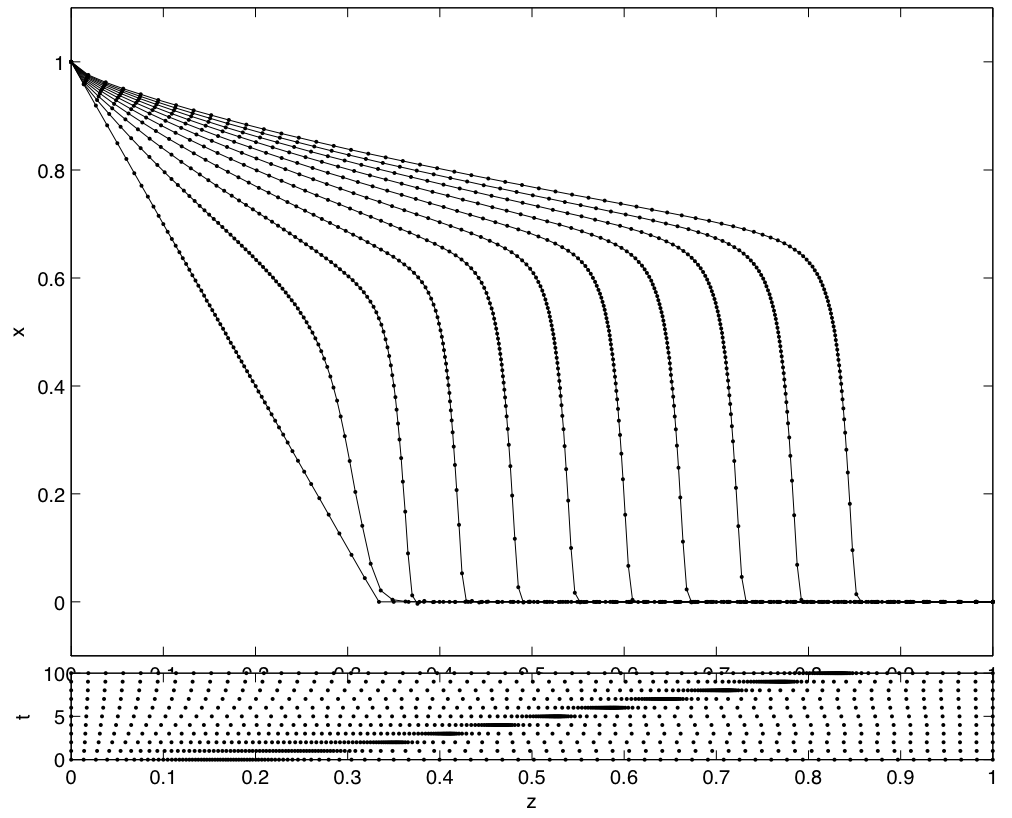
MATMOL contains a set of linear spatial approximation techniques, e.g. finite difference methods, implemented using the concept of differentiation matrices, as well as a set of nonlinear spatial approximations, e.g. flux limiters.

In addition, several time integrators, including basic explicit methods and some advanced linearly implicit methods, are included.

The underlying philosophy of these developments is to provide the user with a variety of easily understood methods, and a collection of application examples that can be used as MATLAB templates for the rapid prototyping of new dynamic simulation codes.

Simulation of ODE/PDE Models with MATLAB®, OCTAVE and SCILAB Scientific and Engineering Applications

Authors: Vande Wouwer, Alain, Saucez, Philippe, Vilas Fernández, Carlos

Simulation of ODE/PDE Models with MATLAB®, OCTAVE and SCILAB shows the reader how to exploit a fuller array of numerical methods for the analysis of complex scientific and engineering systems than is conventionally employed. The book is dedicated to numerical simulation of distributed parameter systems described by mixed systems of algebraic equations, ordinary differential equations (ODEs) and partial differential equations (PDEs)

Link to the Springer web page : https://link.springer.com/book/10.1007/978-3-319-06790-2