Une bourse « ERC consolidator Grant » pour un chercheur de l’UMONS en analyse de données

Nicolas Gillis, professeur dans le service de Mathématique et Recherche Opérationnelle de la Faculté Polytechnique de Mons et brillant détenteur de plusieurs prix scientifiques, vient de décrocher un financement conséquent appelé ERC Consolidator Grant.

Ces bourses de l’European Research Council (ERC) ont une durée de 5 ans et leur  montant peut aller jusqu’à 2 millions d’euro.

Elles sont attribuées à des jeunes chercheurs/chercheuses (7 à 12 ans après leur thèse), leur permettant de consolider leur équipe et développer leur carrière en Europe[1].

Il s’agit donc d’une importante reconnaissance pour la recherche au sein de l’UMONS dans la mesure où cette prestigieuse subvention européenne a pour principal critère de sélection l’excellence scientifique.

Le projet du Prof. Gillis ici retenu est intitulé ‘Beyond Low-Rank Factorizations’ (eLinoR) et porte sur l’amélioration de la performance des systèmes actuels d’analyse de données en changeant leur façon de fonctionner.

Si on considère un ensemble de « points » répartis dans un espace de grande dimension (ces points pouvant représenter des images, des documents, ou encore des évaluations de films par des utilisateurs), approcher ces données via un espace linéaire de plus petite dimension est une technique standard de la littérature.

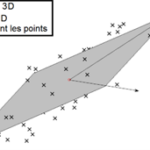
Cette représentation par compression des données en rend la possibilité d’extraction d’information plus aisée. Ces représentations sont obtenues via ce qu’on appelle des techniques de réduction de dimensionalité ; l’analyse en composantes principales (ACP, ou, en anglais, principal component analysis – PCA) étant la plus connue. Voir l’image ci-dessous donnant un exemple pour des points en dimension 3 approchés par un espace linéaire de dimension 2.

Ces techniques sont équivalentes à la factorisation de rang faible d’une matrice (low-rank matrix factorization) dont les colonnes contiennent les « points » du jeu de données. Nicolas Gillis a étudié ces techniques lors de son projet ERC Starting Grant (2016-2021). Bien que ces techniques aient connu et connaissent encore un grand succès, elles ont deux principales limitations : ce sont des modèles linéaires et elles n’apprennent qu’une seule couche de caractéristiques.

Dans ce projet, le chercheur de l’UMONS  va au-delà des factorisations matricielles standard, en considérant des factorisations non linéaires et à plusieurs couches (appelées profondes, ou deep en anglais).

eLinoR se concentrera sur trois aspects fondamentaux :

• Théorie : comprendre ces nouveaux modèles ;
• Algorithmes : mettre au point des algorithmes efficaces ;
• Modèles : concevoir de nouveaux modèles pour des applications spécifiques.

Cette approche unifiée permettra de mieux comprendre ces problèmes, de développer et d’analyser des algorithmes ; puis, de les utiliser pour des applications.

Le but ultime d’eLinoR est de fournir des outils théoriques et algorithmiques pour ces modèles généralisés, permettant de décider quel modèle et quel algorithme utiliser dans quelle situation et quel type de résultat attendre, conduisant à une utilisation généralisée et fiable de ces modèles.

Plusieurs exemples d’applications concrètes dans la vie de tous les jours peuvent être envisagés.

On pourrait par exemple, parmi un réseau de personnes tel que celui composé des abonnés de Facebook, détecter automatiquement des communautés, autrement dit des ensembles de personnes qui interagissent beaucoup. Cette faculté à les identifier pourrait être utilisée à des fins commerciales (marketing de produits) mais aussi médicales (analyse de la propagation d’une épidémie).

La détection de communautés est également utile dans d’autres contextes comme lorsqu’il s’agit d’identifier des groupes de gènes agissant pour des fonctions biologiques similaires[2].

A partir d’un ensemble d’images, on peut vouloir en extraire automatiquement des caractéristiques communes. Par exemple, dans l’illustration ci-dessous, les caractéristiques extraites depuis un grand nombre d’images de visages sont des parties de visages comme les yeux, la bouche, et le nez, et cela à différents niveaux (caractéristiques plus ou moins localisées).

L’imagerie hyperspectrale permet aussi de repérer automatiquement les différents « matériaux » présents dans une image (via des pixels colorés) et de quantifier leurs quantités relatives[3]. Ainsi, par exemple, pour des applications militaires ou de recensement agricole, on peut identifier les routes et les toits des maisons, mais aussi les arbres, l’herbe, les cultures, etc.

On peut aussi songer aux systèmes de recommandations qui, à partir de préférences manifestées par des utilisateurs, ont pour objectif de prédire leurs préférences futures et leurs faire des propositions/suggestions d’autres articles mais aussi de films ou de livres, comme sur les plateformes Netflix ou Amazon.

Enfin, à partir d’un ensemble de documents, on peut les classifier automatiquement en fonction des sujets qu’ils traitent : chaque document va être une combinaison pondérée de sujets[4].

NOTES

[1] https://erc.europa.eu/apply-grant/consolidator-grant

[2] Fortunato, Community detection in graphs, Physics reports 486(3):75-174, 2010.

[3] Ma, Bioucas-Dias, Chan, Gillis, Gader, Plaza, Ambikapathi and Chi, A Signal Processing Perspective on Hyperspectral Unmixing, IEEE Signal Process. Mag. 31(1):67-81, 2014.

[4] Blei, Probabilistic topic models, Communications of the ACM 55(4):77-84, 2012.